Keyword [Stochastic Depth]
Huang G, Sun Y, Liu Z, et al. Deep networks with stochastic depth[C]//European conference on computer vision. Springer, Cham, 2016: 646-661.
1. Overview
1.1. Motivation
Dropout makes the network thinner instead of shorter.
In this paper, it proposes Stochastic Depth
1) For each batch, randomly drop a subset of layers and bypass them with identify function.
2) Deep network during testing, while short network during training.
3) Stochastic Depth during training can be regarded as implicit ensemble of networks with different depth.
4) Speed up training.


2. Stochastic Depth
2.1. Mechanism

$H_l = ReLU(b_l f_l (H_{l-1} + id(H_{l-1})))$.
1) $b_l = 1$. $H_l = ReLU(f_l (H_{l-1} + id(H_{l-1})))$.
2) $b_l=0$. $H_l = id(H_{l-1})$. ($H_{l-1}$ is always non-negative)
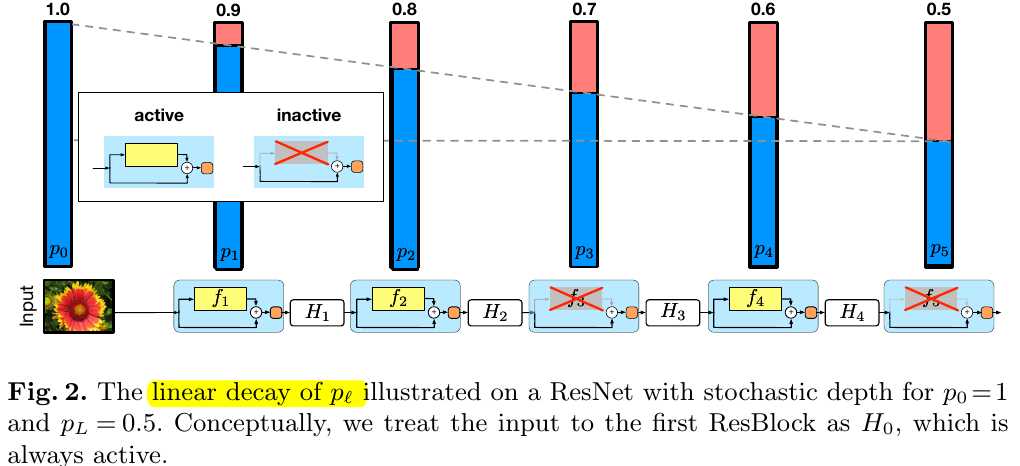
2.2. Survival Probability
1) linear decay rule. $p_l = 1 - \frac{l}{L}(1-P_L)$.
2) In this paper, $P_0.5$.
2.3. Expected Network Depth
$E(\widetilde{L})=\Sigma_{l=1}^L p_l$.
1) When $P_L = 0.5$, $E(\widetilde{L})= (3L - 1) / 4 \approx 3L/4$
2.4. Testing
$H_l^{Test} = ReLU(p_l f_l(H_{l-1}^{Test}; W_l) + H_{l-1}^{Test})$
1) Can be interpreted as combining all possible networks into a single test architecture, in which each layer is weighted by its survival probability.
3. Experiments
